Как найти площадь прямоугольника

Расчет площади земельного участка онлайн калькулятором

На сегодня в сети довольно много сервисов и онлайн-калькуляторов, позволяющих рассчитать площадь земельного участка, достаточно воспользоваться одной из поисковых систем, например Яндекс.

Имейте в виду, что онлайн калькулятору расчета площади понадобится точные размеры всех сторон участка в метрах, чтобы его алгоритм справился с точным расчетом площади вашего участка земли.

Сложнее поддается расчету участок неправильной формы и только лишь размеров сторон будет недостаточно для вычисления площади участка сложной формы. Здесь вам потребуется знать размеры и всех сторон огорода, и размер диагоналей Чуть проще, если один из углов участка составляет 90 градусов.

Вот пример расчета соток земли дачного участка сложной формы:

Размеры сторон земельного участка, в метрах

• Сторона A-B = 69 метров,
• Сторона B-C = 46 метров,
• Сторона C-D = 87 метров,
• Сторона D-A = 35 метров,
• Левый нижний угол прямой (90 градусов)

По этим данным можно определить длины диагоналей B-D и A-C, и рассчитать площадь участка = 3035 квадратных метров (или 30,35 соток).

Для того, чтобы определить количество соток на участке, нужно его каким-нибудь способом измерить. Некоторые люди могут сказать «на глаз» какой размер территории — это те, у кого есть опыт в подобных делах. А большинство же такой возможности не имеет. Что же делать, как быть в подобной ситуации? Как рассчитать размер участка, можно узнать из этой статьи.

Для начала нужно определиться с тем, в каких единицах измерять нужную территорию. Это могут быть метры квадратные, сотки или гектары. Разберем все эти единицы измерения. Гектар равен 100 соткам, сотка равна 100 квадратным метрам. Измерять один гектар еще можно, но если их десятки, а то и сотни — сделать это без оборудования достаточно сложно.

Метр квадратный достаточно мелкая единица измерения для участка. Метры больше подходят для помещений, домов и квартир. Оптимальным параметром для небольшого участка является сотка. Итак, сотка — это 10 метров на 10 метров (100 метров квадратных) . Значит, для того, чтобы рассчитать сотки, нужно определить, как и чем сделать замеры.

Сделать это можно несколькими способами. Один из них — это посредством шагового измерения. Перед тем, как это сделать, нужно учесть, что шаги у всех разные. Стоит определить для себя, какое расстояние обозначает один метр и потренировать ноги на заданное расстояние. Обычно — это один широкий шаг человека, без прыжка. Или же измерить свободный шаг в сантиметрах и перевести в метры (например, 0,7 м) .

Значит, для того, чтобы приблизительно измерить сотку нужно сосчитать шаги по периметру участка: длину и ширину. После этого умножить одну цифру на другую и получится площадь территории в метрах квадратных. Например, длинна 60 шагов (метров) , а ширина 30 шагов (метров) — умножив, получилась цифра 1800 метров квадратных. Далее, разделив на 100 (одна сотка — это 100 метров квадратных) , получается 18 соток.

Еще один способ измерить участок, более точный — это соорудить палку, длинной в метр или 2 (3) . И таким образом сделать замеры. Наиболее точной длину палки можно сделать при помощи роста тела или же какого-либо предмета, размер которого известен. Это может быть тротуарная плитка (обычно 30 см) , столбик ограждения или же можно измерить растяжкой большого и указательного пальца (приблизительно 20 см) .

Как рассчитать сотку земли при помощи палки? Очень просто. Так же, как и шагами: отмерять 10 раз палкой в длину и ширину — вот и получится одна сотка. Далее нужно сложить всю площадь измерений, чтобы знать количество соток на всем участке. Для удобства к палке можно прикрепить еще две — в виде треугольника, таким образом можно «шагать» этим измерителем. И более точно произвести все замеры.

Самым точным и оптимальным способом измерения участка — сделать это при помощи рулетки. Измерить периметр в метрах, а потом перевести в сотки. Но для этого нужно подготовиться и иметь такой прибор в распоряжении. Но такое не всегда возможно, поэтому вышеперечисленные способы являются весьма хорошими и применимыми на практике. Главное во всем этом — уметь хорошо считать и переводить размеры в уме. Только так можно справиться с этой задачей.

Что такое сотка, ар, гектар, квадратный километр? Сколько гектар, квадратных метров и километров в одном аре (сотке) земли? Сколько квадратных метров, километров и соток в одном гектаре земли? Сколько соток, гектар и квадратных метров в одном квадратном километре?

Калькулятор расчета площади земельного участка неправильной формы

Инструкция для калькулятора расчета площади неправильного земельного участка

Данный онлайн калькулятор помогает произвести расчет, определение и вычисление площади земельного участка в онлайн режиме. Представленная программа способна правильно подсказать, как выполнить расчет площади земельных участков неправильной формы.

Указываем все данные в метрах

A B, D A, C D, B C— Размер каждой стороны делянки.

Согласно введен данным, наша программа в онлайн режиме выполнить расчет и определить, площадь земельных угодий в квадратных метрах, сотках, акрах и гектарах.

Методика определения размеров участка ручным методом

Чтобы правильно выполнить расчет площади делянок, не нужно использовать сложные инструменты. Мы берем деревянные колышки или металлические прутья и устанавливаем их в углах нашего участка. Далее при помощи измерительной рулетки определяем ширину и длину делянки. Как правило, достаточно выполнить замер одной ширины и одной длины, для прямоугольных или равносторонних участков. Для примера, у нас получились следующие данные: ширина – 20 метров и длина – 40 метров.

Далее переходим к расчету площади делянки. При правильной форме участка, можно использовать геометрическую формулу определения площади (S) прямоугольника. Согласно этой формуле, нужно выполнить умножение ширины (20) на длину (40) , то есть произведение длин двух сторон. В нашем случае S=800 м².

После того, как мы определили нашу площадь, мы можем определить количество соток на земельном участке. Согласно общепринятым данным, в одной сотке – 100 м². Далее при помощи простой арифметики, мы разделим наш параметр S на 100. Готовый результат и станет равен размеру делянки в сотках. Для нашего примера, этот результат – 8. Таким образом, получаем, что площадь участка составляет восемь соток.

В том случае, когда территория угодий очень большая, то лучше всего выполнять все измерения в других единицах – в гектарах. Согласно общепринятым единицам измерения – 1 Га = 100 соток. К примеру, если наша земельная делянка согласно полученным измерениям составляем 10 000 м², то в этом случае его площадь равна 1 гектару или 100 соткам.

Если Ваш участок неправильной формы, то в этом случае количество соток напрямую зависит от площади. Именно по этой причине при помощи онлайн калькулятора Вы сможете правильно рассчитать параметр S делянки, и после этого разделив полученный результат на 100. Таким образом, Вы получите расчеты в сотках. Такой метод предоставляет возможность измерять делянки сложных форм, что весьма удобно.

Общие данные

Расчет площади земельных участков базируется на классических расчетах, которые выполняются согласно общепринятым геодезическим формулам.

Всего доступно несколько методов для расчета площади земельных угодий – механический (рассчитывается по плану при помощи мерных палеток), графический (определяется по проекту) и аналитический (при помощи формулы площади по измеренным линиям границ).

На сегодняшний день самым точным способом заслуженно считается – аналитический. Используя данный метод, ошибки при расчетах, как правило, появляются из-за погрешностей на местности измеренных линий. Данный способ является также и достаточно сложным, если границы криволинейные или количество углом на делянке больше десяти.

Немного проще по расчетам является графическим способ. Его лучше всего использовать в том случае, когда границы участка представлены в виде ломанной линии, с небольшим количеством поворотов.

И самый доступный и простой способ, и наиболее популярный, но и в тоже время самой большой погрешностью – механический способ. Используя данный метод, Вы сможете легко и быстро выполнить расчет площади земельных угодий простой или сложной формы.

Среди серьезных недостатков механического или графического способа, выделяют следующее, кроме погрешностей при измерении участка, при расчетах добавляется погрешность из-за деформации бумаги или погрешность при составлении планов.

Источник

Площадь равнобедренной трапеции

1. Формула площади равнобедренной трапеции через стороны и угол

b — верхнее основание

a — нижнее основание

c — равные боковые стороны

α — угол при нижнем основании

Формула площади равнобедренной трапеции через стороны, (S):

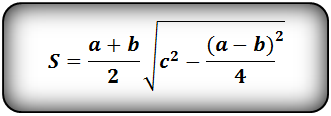
Формула площади равнобедренной трапеции через стороны и угол, (S):

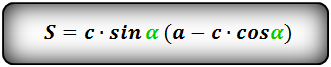
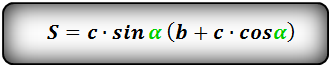
2. Формула площади равнобокой трапеции через радиус вписанной окружности

R — радиус вписанной окружности

D — диаметр вписанной окружности

O — центр вписанной окружности

H — высота трапеции

α , β — углы трапеции

Формула площади равнобокой трапеции через радиус вписанной окружности, (S):

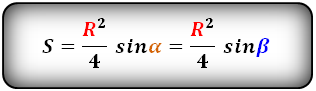
СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d — диагональ трапеции

α , β — углы между диагоналями

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

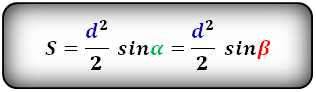
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

m — средняя линия трапеции

c — боковая сторона

α , β — углы при основании

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

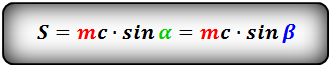
5. Формула площади равнобедренной трапеции через основания и высоту

b — верхнее основание

a — нижнее основание

h — высота трапеции

Формула площади равнобедренной трапеции через основания и высоту, (S):

Источник

Определение площади сложной фигуры с помощью теории вероятностей

Да мало ли зачем. Например, возникла необходимость определить площадь территории на карте.

Конечно, можно посмотреть в справочнике или поискать в интернете, но иногда и территории бывают нестандартными — допустим, вы озаботились проблемами лесов в пойме Амазонки и хотите ежемесячно измерять площадь зелёных пятен на фотографиях со спутника.

Если вы ботаник (в хорошем смысле слова), то вам может понадобиться измерить площадь листовой поверхности разных сортов одного растения. Или, к примеру, более прозаичная задача — нужно зашпатлевать кусок стены, а банки шпатлёвки хватает только на 1 кв. м. — нужно выяснить, покупать одну банку или раскошелиться на две.

В чём сложность нахождения площади?

Конечно, если фигура представляет собой прямоугольник, круг или, что хуже, эллипс, то проблема решается с помощью Google и калькулятора. Но где бы найти формулу, да попроще, для нахождения площади, скажем, такого рисунка?

Теория вероятностей, Ваш выход!

Сразу оговорюсь, что теория вероятностей по своей сути не подразумевает точного решения задач. Так будет и в этом случае — если вам нужна космическая точность, то предлагаю копать в сторону методов имитационного моделирования. Если же погрешность в пределах 2-5% вас вполне устраивает, то будет достаточно того же калькулятора, базовых навыков программирования и умения считать до ста.

Суть метода

Суть метода проста до банальности. Допустим, мы пасмурным деньком выложили капустный листочек (см. ремарку про биолога выше) на прямоугольный поддон, а поддон выставили под накрапывающий дождик.

А потом засекли определённое время (к примеру, пять минут) и посчитали, сколько капелек упало на поддон, а сколько непосредственно на лист.

Если принять во внимание, что дождь обычно капает равномерно, то получается простая пропорция — лист во столько раз меньше поддона, во сколько раз на него упало меньше капель дождя, чем на весь поддон

Возвращаемся к нашей фигуре

Итак, как же определить площадь той розовой пятерни? Да очень просто — заключить фигуру в прямоугольные границы и проставить случайным образом много точек. Чем больше, тем лучше (в соответствии с законом больших чисел). А потом подсчитать количество точек, попавших на фигуру.

Я намеренно не обсуждаю вопросы реализации такого алгоритма, потому что вариантов масса. Можно просто закрыть глаза и наугад тыкать шариковой ручкой, а можно действовать более научно — с помощью языков программирования.

Например, код на PHP занял у меня не больше 15 строчек, а в результате получилось вот что: Точки общим числом 300, разумеется, проставлены с помощью генератора случайных чисел.

Для удобства подсчета точек я разбил изображение на 36 секторов — теперь нужно подсчитать количество точек, попавших на изображение, в каждом секторе, а результаты сложить.

Сведём данные в таблицу (ячейка таблицы соответствует сектору на картинке):

4	8	4
7	5	6	4
3	6	13	7	8	5
1	10	10	13	7	2
2	3	7	10	2
2	5	3

Теперь у нас есть все данные для того, чтобы вычислить площадь розовой пятерни: площадь описанного прямоугольника — 20 см х 20 см = 400 кв. см; количество точек в прямоугольнике — 300; количество точек внутри фигуры (сумма значений из таблицы) — 157;

площадь фигуры – 209,33 кв. см.

И насколько это точно?

Действительно, осталось определиться с точностью данного метода. Конечно, всё зависит от количества точек, и здесь нужно соблюдать золотую середину — десяти для нашего примера было бы явно недостаточно, а от тысячи слишком рябило бы в глазах. Поэтому попробуем определить погрешность для трёхсот точек и описанного квадрата со стороной 20 см.

Для этого возьмём фигуру, площадь которой нам известна заранее.

Например, такую: Проставляем точки: Результаты заносим в таблицу:

6	11	8	5
9	15	8	5	13	2
11	8	5	14	13	5
10	11	8	8	4	4
2	14	9	10	4	1
3	5	6

Рассчитываем площадь фигуры: площадь описанного прямоугольника — 20 см х 20 см = 400 кв. см; количество точек в прямоугольнике — 300; количество точек внутри фигуры (сумма значений из таблицы) — 237;

площадь фигуры – 316 кв. см.

Нетрудно посчитать, что реальная площадь круга с радиусом 10 см составляет 314,16 кв. см. Таким образом, погрешность метода составила 0,59%, чего в большинстве случаев достаточно для прикладного использования.

• теория вероятностей
• площадь фигуры

Хабы:

Формулы для площадей четырехугольников

Четырехугольник	Рисунок	Формула площади	Обозначения
		S = ab	a и b – смежные стороны
		d – диагональ,φ – любой из четырёх углов между
	S = 2R2 sin φ Получается из верхней формулы подстановкой d=2R	R – радиус ,φ – любой из четырёх углов между
		S = a ha	a – сторона,ha – , опущенная на эту сторону
	S = absin φ	a и b – смежные стороны,φ – угол между ними
		d1, d2 – , φ – любой из четырёх углов между ними
		S = a2	a – сторона квадрата
	S = 4r2	r – радиус
		d – квадрата
	S = 2R2 Получается из верхней формулы подстановкой d = 2R	R – радиус
		S = a ha	a – сторона,ha – , опущенная на эту сторону
	S = a2 sin φ	a – сторона,φ – любой из четырёх углов ромба
		d1, d2 –
	S = 2ar	a – сторона,r – радиус
		r – радиус ,φ – любой из четырёх углов ромба
			a и b – основания,h –
	S = m h	m – ,h –
		d1, d2 – , φ – любой из четырёх углов между ними
		a и b – основания,c и d  – боковые стороны
		S = ab sin φ	a и b – неравные стороны,φ – угол между ними
		a и b – неравные стороны,φ1 – угол между сторонами, равными a ,φ2 – угол между сторонами, равными b.
	S = (a + b) r	a и b – неравные стороны,r – радиус
		d1, d2 –
Произвольный выпуклый четырёхугольник			d1, d2 – , φ – любой из четырёх углов между ними
		,	a, b, c, d – длины сторон четырёхугольника,p – , Формулу называют «Формула Брахмагупты»

	S = ab гдеa и b – смежные стороны
	гдеd – диагональ,φ – любой из четырёх углов между
	S = 2R2 sin φ гдеR – радиус ,φ – любой из четырёх углов между Формула получается из верхней формулы подстановкой d = 2R
	S = a ha гдеa – сторона,ha – , опущенная на эту сторону
	S = absin φ гдеa и b – смежные стороны,φ – угол между ними
	гдеd1, d2 – , φ – любой из четырёх углов между ними
	S = a2 гдеa – сторона квадрата
	S = 4r2 гдеr – радиус
	гдеd – квадрата
	S = 2R2 гдеR – радиус Получается из верхней формулы подстановкой d = 2R
	S = a ha гдеa – сторона,ha – , опущенная на эту сторону
	S = a2 sin φ гдеa – сторона,φ – любой из четырёх углов ромба
	гдеd1, d2 –
	S = 2ar гдеa – сторона,r – радиус
	гдеr – радиус ,φ – любой из четырёх углов ромба
	гдеa и b – основания,h –
	S = m h гдеm – ,h –
	гдеd1, d2 – , φ – любой из четырёх углов между ними
	гдеa и b – основания,c и d  – боковые стороны
	S = ab sin φ гдеa и b – неравные стороны,φ – угол между ними
	гдеa и b – неравные стороны,φ1 – угол между сторонами, равными a ,φ2 – угол между сторонами, равными b.
	S = (a + b) r гдеa и b – неравные стороны,r – радиус
	гдеd1, d2 –
Произвольный выпуклый четырёхугольник
	гдеd1, d2 – , φ – любой из четырёх углов между ними
	, гдеa, b, c, d – длины сторон четырёхугольника,p – Формулу называют «Формула Брахмагупты»

S = ab гдеa и b – смежные стороны

гдеd – диагональ,φ – любой из четырёх углов между

S = 2R2 sin φ гдеR – радиус ,φ – любой из четырёх углов между Формула получается из верхней формулы подстановкой d = 2R

S = a ha гдеa – сторона,ha – , опущенная на эту сторону

S = absin φ гдеa и b – смежные стороны,φ – угол между ними

гдеd1, d2 – , φ – любой из четырёх углов между ними

S = a2 гдеa – сторона квадрата

S = 4r2 гдеr – радиус

гдеd – квадрата

S = 2R2 гдеR – радиус Получается из верхней формулы подстановкой d = 2R

S = a ha гдеa – сторона,ha – , опущенная на эту сторону

S = a2 sin φ гдеa – сторона,φ – любой из четырёх углов ромба

гдеd1, d2 –

S = 2ar гдеa – сторона,r – радиус

гдеr – радиус ,φ – любой из четырёх углов ромба

гдеa и b – основания,h –

S = m h гдеm – ,h –

гдеd1, d2 – , φ – любой из четырёх углов между ними

гдеa и b – основания,c и d  – боковые стороны,

S = ab sin φ гдеa и b – неравные стороны,φ – угол между ними

гдеa и b – неравные стороны,φ1 – угол между сторонами, равными a ,φ2 – угол между сторонами, равными b.

S = (a + b) r гдеa и b – неравные стороны,r – радиус

гдеd1, d2 –

Произвольный выпуклый четырёхугольник

гдеd1, d2 – , φ – любой из четырёх углов между ними

гдеa, b, c, d – длины сторон четырёхугольника,p – Формулу называют «Формула Брахмагупты»

Общие сведения

В различных задачах с физико-математическим уклоном приходится вычислять площадь прямоугольника. Однако формула расчета применяется не только в математике и физике, но и во время ремонтных работ. Например, следует посчитать количество расходных материалов, которое зависит от квадратуры комнаты или здания.

Очень важно не только знать основные соотношения, но и корректно переводить единицы измерения из одной в другую. От знаний полностью зависит экономия денежных средств

Например, при клейке обоев в комнате требуется определенное количество рулонов. Это количество можно купить в строительном магазине «на глаз» или рассчитать квадратуру комнаты. Во втором случае можно существенно сэкономить. Для того чтобы посчитать квадратные метры помещения, нужно вычислить его площадь.

Площадь фигуры

Площадью двумерной фигуры является численная характеристика, которая показывает ее размерность. Она обозначается литерой S и измеряется в квадратных единицах (мм 2 , см 2 , дм 2 и т. д.). Не каждый элемент геометрии имеет площадь. Прямая, луч, отрезок, точка не имеют двумерной размерности. Фигуры, у которых она присутствует, являются квадратируемыми. Если значения их S равны, то они являются равновеликими.

Для вычисления значения двухплоскостной размерности фигуры применяется интегральный метод. Однако бывают частные случаи, когда вычислять интеграл необязательно. Существуют определенные формулы, полученные с помощью интегрального метода. Чтобы ими воспользоваться, нужно просто подставить числовые значения сторон.

Единицы измерения

При решении задач на нахождение значения площади нужно знать единицы ее измерения. Кроме того, следует правильно выполнять перевод одной единицы в другую. В системе исчисления используются квадратичные единицы измерения. За основу следует брать размер стороны прямоугольника. Например, при указании площади в кв. м нужно измерять в метраже стороны объекта. Это стандартная единица измерения площади.

Существуют также производные единицы. Самой маленькой из них является квадратный миллиметр (кв. мм или мм 2 ). В некоторой литературе или программировании можно встретить такую запись: sqr (m), которая означает квадратный метр. Основные производные единицы площади:

1 см 2 = 100 мм 2 .

1 дм 2 = 100 см 2 .

1 м 2 = 100 дм 2 = 10000 см 2 .

1 км 2 = 1000000 м 2 .

1 ар (а) = 1 сотка = 100 м 2 .

1 гектар (га) = 10000 м 2 .

Последние применяются для измерения земельного участка. Однако необязательно их все помнить. Они легко выводятся при помощи простейших математических вычислений. Например, для выполнения расчетов нужно перевести кв. м в кв. см. Однако человек мог забыть, сколько см 2 в квадратном метре. Следует взять метрическую форму (1 м = 100 см). Затем нужно возвести обе части выражения в квадрат: 1 м 2 = 100 * 100 = 10000 (см 2 ).

Обозначение площади

Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.

Если параметры фигуры переданы в разных единицах длины, мы не сможем решить ни одну задачу. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

Популярные единицы измерения

• квадратный миллиметр (мм 2 );
• квадратный сантиметр (см 2 );
• квадратный дециметр (дм 2 );
• квадратный метр (м 2 );
• квадратный километр (км 2 );
• гектар (га).

Круг — это когда множество точек на плоскости удалены от центра на равном радиусу расстоянии. Радиусом принято называть прямую линию, соединяющую центр с любой точкой окружности.

1. S = π * r 2 , где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

2. S = d 2 : 4 * π, где d — это диаметр.

3. S = L 2 ​ : 4 * π, где L — это длина окружности.

Как найти площадь неправильной фигуры | Сделай все сам

В школьном курсе геометрии ученики в основном считают площади положительных многоугольников. Между тем, для решения множества фактических задач неоднократно доводится иметь дело с неправильными геометрическими фигурами.

С этой задачей человек сталкивается и при определении размеров дачного участка либо придомовой территории, и при расчете числа ткани для шитья, и еще во многих случаях.

Высчитать площадь неправильной фигуры дозволено несколькими методами.

Вам понадобится

• – неправильная геометрическая фигура;
• – измерительные инструменты;
• – прозрачный пластик;
• – линейка;
• – угольник;
• – шариковая ручка.

Инструкция

1. Разглядите геометрическую фигуру и определите, какие ее параметры вам вестимы. Это могут быть длины сторон либо углы. В зависимости от заданных параметров и выберите метод определения площади. Скажем, поделите ее на несколько фигур, формулы вычисления площади которых вы знаете.

Один из самых распространенных способов — провести диагонали из одного угла ко каждым остальным вершинам. В этом случае вам необходимо знать формулу вычисления площади произвольного треугольника. Но никто не воспрещает поделить заданную фигуру и на другие многоугольники.

Скажем, при расчете площади пола в комнате с нишей комфортнее поделить неправильную фигуру на два прямоугольника либо квадрата.

2. Для определения площади не слишком огромный детали дозволено воспользуйтесь палеткой. Ее дозволено сделать самому. Отрежьте прямоугольный кусок всякого прозрачного пластика.

Поделите его на квадраты, площадь которых вам вестима — скажем, 1х1 либо 0,5х0,5 см. Линейка и угольник обязаны быть точными. Наложите палетку на деталь. Сосчитайте полные квадратики, после этого — неполные.

Роль палетки будет исполнять сетка из квадратов со стороной 1х1 м, начерченная на земле либо подмеченная колышками с протянутыми между ними шнурами. Дозволено ограничиться и разметкой территории на полосы. .

3. С большими площадями дозволено поступить и напротив. Возьмите максимально точный план участка либо придомовой территории. Определите масштаб. Воспользуйтесь одним из предложенных методов. После этого полученное число квадратных сантиметров переведите в надобный масштаб.

Перед тем как начинать ремонт пола в доме, нужно узнать всеобщую площадь , дабы верно рассчитать число материала. Несложная, казалось бы, задача на деле может вызвать много сложностей. Дабы положительно обнаружить площадьпола , вам нужно знать некоторые нюансы измерительной науки.

Вам понадобится

• – рулетка;
• – электронный дальномер;
• – лист бумаги и карандаш;
• – калькулятор.

Примеры решения

Задачи на нахождение площади применяются в нескольких дисциплинах. В геометрии применяются различные комбинации, при которых известны некоторые величины:

1. Две стороны.
2. Одна из сторон и диагональ.
3. Диагональ и разность сторон.

Для расчета расходных материалов и площади поперечного сечения проводника можно всегда измерить стороны прямоугольника. Существует два способа нахождения: автоматизированный и ручной. В первом случае используется специализированное программное обеспечение. Однако вовсе не обязательно применять сложные алгоритмы и программные модули, поскольку формула является очень простой. Для расчета специалисты рекомендуют применять онлайн-калькулятор.

При ручном режиме расчета нужно подставлять значения в формулу. После этого выполнять вычисления. Возможна и оптимизация процесса вычисления. Для этой цели рекомендуется использовать Excel. Приложение входит в состав стандартного офисного пакета MS Office.

Геометрия на плоскости

Задача сводится к тому, что необходимо высчитать S, зная размеры сторон (a = 25 и b = 10). В этом случае следует воспользоваться базовой формулой: S = a * b = 25 * 10 = 250 (ед 2 ). В ответе указывается условная единица измерения, поскольку явная не указана в условии задачи.

Еще один вариант задания немного сложнее предыдущего. Он имеет следующее условие: одна из сторон прямоугольника равна 6 м и диагональ 10 м. Нужно найти площадь прямоугольника. Формулой в этом случае является теорема Пифагора. Треугольник, который образуется при проведении диагонали, считается прямоугольный (неравносторонний, а разносторонний). Решается задача следующим образом:

Находится неизвестная сторона: b =(d 2 — a 2 )^(1/2) = (100 — 36)^(1/2) = 8 (м).

Площадь (произведение сторон): S = 6 * 8 = 48 (м 2 ).

Можно использовать двойную формулу Герона, однако метод усложняет вычисления. Для сравнения скорости и объема вычислений следует решить задачу вторым способом:

Значение площади будет вычисляться таким образом: S = 2 * ^(1/2) = 2 * 24 = 48 (м 2 ).

Второй способ считается неправильным, поскольку необходимо во всех задачах оптимизировать вычисления. Сложным типом задачи, кроме интегрирования, считается нахождение площади, когда неизвестны стороны, а известна только диагональ (10). Известно также, что одна из сторон больше другой на 3 метра. В этом случае надо выражать одну сторону через другую. Алгоритм решения следующий:

1. Обозначить стороны: a = x и b = x — 3.
2. Составить уравнение: x * (x — 3) = 10.

Раскрыть скобки: x 2 — 3x — 10 = 0.

Нахождение дискриминанта: D = b 2 — 4* a * c = 9 — (4 * 10) 2 ). Однако берется не исходное значение, а приближенное. Его нужно округлять только в большую сторону, т. е. править 3,75 на значение 4. Следует руководствоваться таким правилом: результат округляется в большую сторону.

Источник

Вычислить, найти площадь геометрических фигур

Онлайн Расчеты и формулы площади для плоских фигур
Площадь треугольника калькулятор нахождения площади треугольников	Площадь прямоугольного треугольника онлайн формула площади прямоугольного треугольника
Площадь равнобедренного треугольника найти площади равнобедренных треугольников	Площадь равностороннего треугольника вычислить площадь равностороннего треугольника
Площадь треугольника по формуле Герона площадь Герона, формула	Площадь квадрата чему равна площадь квадрата
Площадь прямоугольника как найти чему равна площадь прямоугольника	Площадь круга онлайн калькулятор площади круга через радиуса
Площадь ромба как найти площадь ромба через диагонали и т.д.	Площадь параллелограмма онлайн калькулятор для нахождения площади параллелограмма
Площадь трапеции площадь прямоугольной и равнобедренной трапеции	Площадь эллипса формула площади эллипса онлайн
Площадь кольца как вычислить площадь кольца онлайн	Площадь четырехугольника чему равна площадь четырехугольника, формула
Площадь сектора кольца подсчитать площади сектора кольца	Площадь сектора круга получить площадь сектора круга
Площадь сегмента круга решить площадь сегмента круга
Онлайн Расчеты и формулы площади для объемных фигур
Площадь шара калькулятор нахождения площадь поверхности сферы или шара	Площадь куба как найти чему равна площадь поверхности куба
Площадь цилиндра калькулятор для нахождения площади поверхности и основания цилиндра	Площадь пирамиды формулы расчета площади боковой поверхности и основания пирамиды
Площадь параллелепипеда калькулятор площади параллелепипеда прямоугольного и др.	Площадь конуса нахождение площади поверхностей конуса
Площадь усеченного конуса калькулятор нахождения площади поверхности усеченного конуса	Площадь тетраэдра площадь поверхности и грани тетраэдра
Площадь призмы калькулятор нахождения площади поверхности и боковой площади призмы

Площадь фигуры сложной формы может составляться из различных элементарных фигур: треугольников, квадратов, прямоугольников и пр. Общая площадь будет высчитываться путем суммирования площадей составляющих компонент.

Набор онлайн-калькуляторов страницы дает возможность оперативного вычисления не только S плоских фигур (квадрата, прямоугольника, круга, ромба, эллипса), но и площадей объемных фигур (куба, призмы, конуса, цилиндра, сферы, тетраэдра и пр.), являющихся совокупностью нескольких плоскостей.

Вычисление площадей фигур востребовано для решения различных задач: — строительных; — кадастровых; — инженерных и пр.

Государство осуществляет кадастровый учет земельных участков, основным учитываемым параметром которых является площадь. Специалистами БТИ фиксируется общая и полезная жилая площадь квартир. В быту иногда нужно вычислять площадь ковра, натяжного потолка, площадь дачного участка и пр.

Источник

Инструкция для калькулятора расчета площади земельного участка неправильной формы

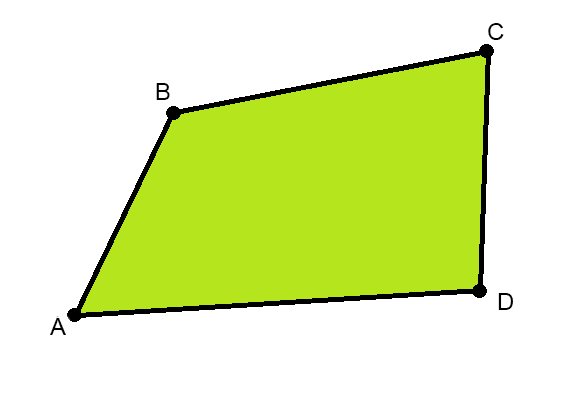
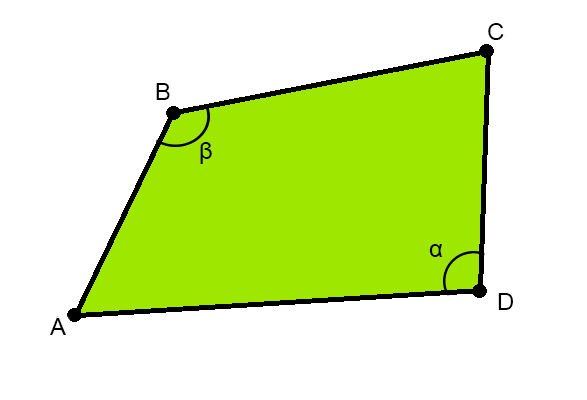
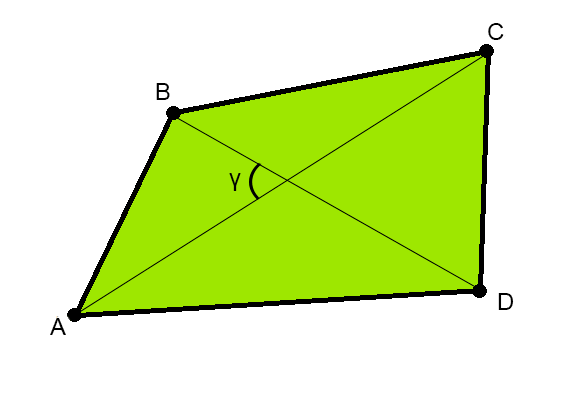
Впишите размеры сторон AB, BC, CD, DA в метрах.

Замеры участка проводят, с помощью длинной рулетки, лазерного дальномера, мерного колеса. Также можно изготовить деревянную треногу (наподобие циркуля) зафиксировав расстоянием между «ногами» в 1 м и, шагая таким приспособлением вдоль границы делянки подсчитать количество шагов.

Нажмите «Рассчитать».

Онлайн калькулятор позволяет определить площадь (в квадратных метрах, сотках, акрах и гектарах) земельного участка или поля, имеющего неправильную форму. Это пригодится для корректного оформления документов права собственности на землю, продажи, сдачи в аренду или его деления (т.н. межевания) без применения топографической съемки и специальных картографических программ. Также иногда просто нужно посчитать сколько соток имеет участок, чтобы прикинуть его рыночную стоимость.

Источник

Вывод формул для площадей четырехугольников

      Утверждение 1. Площадь выпуклого четырёхугольника можно найти по формуле

где  d₁ и d₂ – , а φ – любой из четырёх углов между ними (рис. 1).

Рис. 1

      Доказательство. В соответствии с рисунком 1 справедливо равенство:

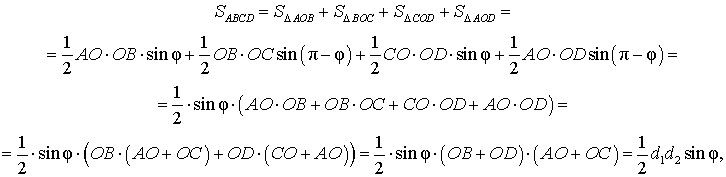
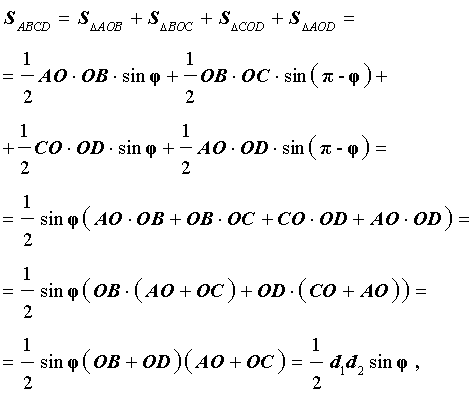
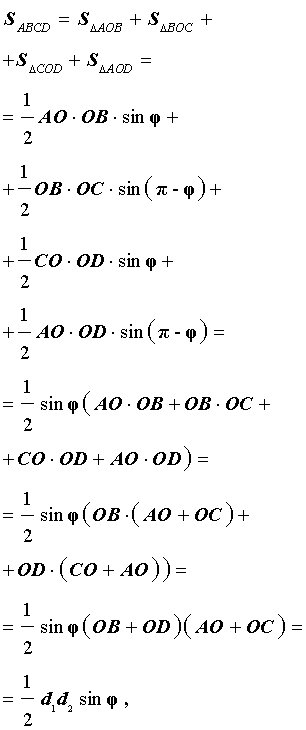
что и требовалось доказать.

      Утверждение 2. Площадь можно найти по формуле

S = a h_a ,

где a – сторона параллелограмма, а h_a – , опущенная на эту сторону (рис. 2).

Рис. 2

      Доказательство. Поскольку (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому

S_ABCD = S_AEFD = a h_a ,

что и требовалось доказать.

      Утверждение 3.Площадь можно найти по формуле

S = ab sin φ,

где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).

Рис. 3

      Доказательство. Поскольку

h_a = b sin φ,

то, в силу утверждения 2, справедлива формула

S = a h_a = ab sin φ,

что и требовалось доказать.

      Утверждение 4. Площадь можно найти по формуле

,

где r – радиус , а φ – любой из четырёх углов ромба (рис.4).

Рис. 4

      Доказательство. Поскольку каждая из ромба является биссектрисой угла, а . Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому

что и требовалось доказать.

      Утверждение 5. Площадь можно найти по формуле

,

где a и b – основания трапеции, а h  –  (рис.5).

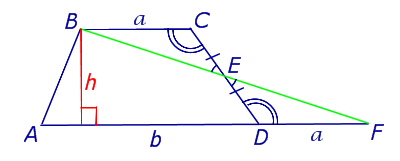
Рис. 5

      Доказательство. Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD. Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку , то площадь трапеции ABCD равна площади треугольника ABF. Поэтому

что и требовалось доказать.

      Утверждение 6. Площадь можно найти по формуле

,

где a и b – основания, а c и d – боковые стороны трапеции, (рис.6).

Рис. 6

      Доказательство. Воспользовавшись , составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

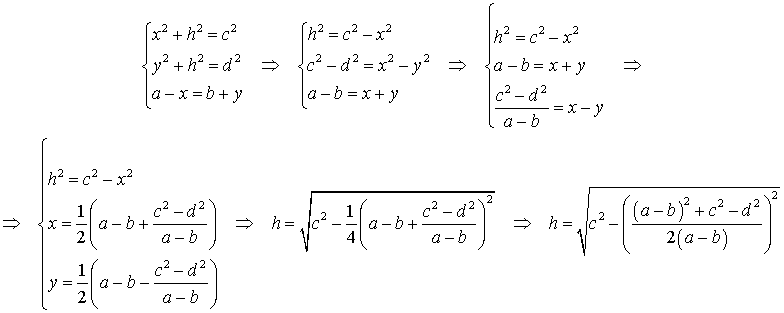
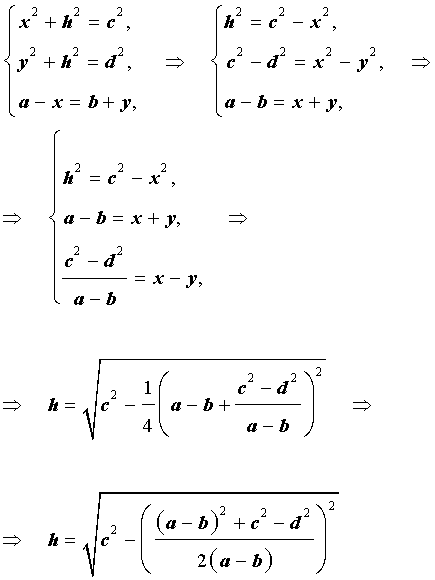
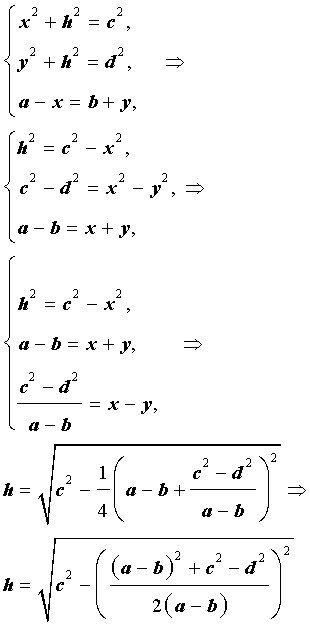
      Следовательно,

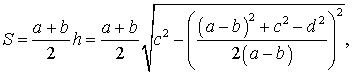
где

,

что и требовалось доказать.

      Утверждение 7. Площадь , , можно найти по формуле:

S = (a + b) r,

где a и b – неравные стороны дельтоида, а r – радиус (рис.7).

Рис. 7

      Доказательство. Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D, а биссектрисы углов A и C пересекаются в некоторой точке O, лежащей на диагонали BD. Точка O и является центром вписанной в дельтоид окружности.

      Если r – радиус вписанной в дельтоид окружности, то

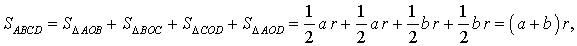
что и требовалось доказать.